Funktionenlupe I - das Funktionenmikroskop 2.0

In linken Fenster ist der Graph einer Funktion f im Standard-Zoom zu sehen. Um einen Punkt A auf dem Graphen ist ein Quadrat hervorgehoben, das sich von A aus um h nach links, rechts, unten und oben erstreckt. Die Größe dieses Quadrats kann über den Schieberegler h verändert werden. Dieses Quadrat wird dann in das zweite Fenster vergrößert kopiert, so dass es dort immer den gleichen Platz ausfüllt. 

Die Grenzen zwischen den Fenstern sollten so gezogen werden, dass das rechte Lupenfenster auch quadratisches Format hat (das ist abhängig von der Software und der jeweiligen Bildschirmauflösung).

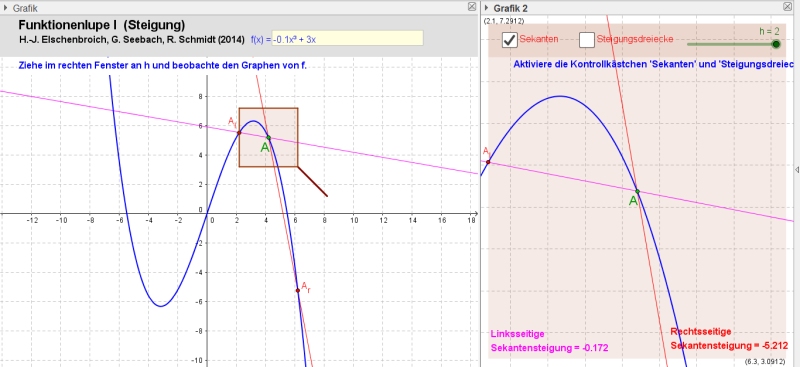
Die Funktionenlupe I mit h = 2.

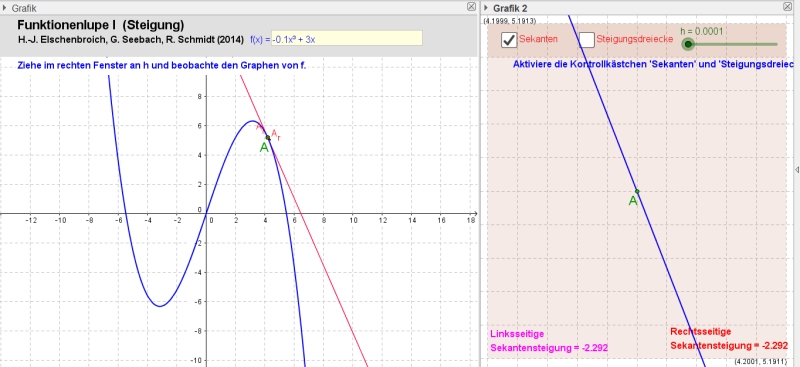
Die Funktionenlupe I mit h = 0.0001.

Wird h immer weiter verkleinert, bis h = 0.0001, so sieht man, dass der Graph von f dann im rechten Fenster praktisch gerade aussieht. Dies ist die digitale Umsetzung des Funktionenmikroskops von Kirsch.

Die Funktionenlupe bietet zusätzlich die Möglichkeit, sich die Sekanten und die Steigungsdreiecke anzeigen zu lassen und diese Steigungen zu ermitteln. Dabei haben wir links von A = (x_a, y_a) den Punkt A_l auf dem Graphen von f, dessen x-Koordinate x_a-h ist und rechts von A den Punkt A_r auf dem Graphen von f, dessen x-Koordinate x_a+h ist. Die linksseitige Sekante verläuft durch A_l und A, die rechtsseitige Sekante durch A und A_r. 

Damit dockt man an die üblichen Zugänge im Mathematikunterrichts (Sekante, h-Methode) an. Man sieht dann bei Verkleinerung von h, dass die beiden Sekanten anschaulich zusammenfallen und eine Schmiegegerade bilden (die dann als Tangente deklariert wird). Bemerkenswert und didaktisch fruchtbar ist insbesondere, dass hier bei Veränderung von h beide Sekanten simultan verändert werden und der Prozess des Einschachtelns der Tangente durch die Sekanten eindrucksvoll sichtbar wird.

Hier haben wir also zum einen den Effekt des Hineinzoomens und behalten zum anderen den Überblick. Desweiteren kann man an A ziehen und man kann einen anderen Funktionsterm wählen. Damit erhalten wir mit der Funktionenlupe I einen anschaulichen und kalkülfreien Zugang zur lokalen Steigung, jedenfalls bei schultypischen 'gutartigen' Funktionen.  

Auf eins sei noch hingewiesen: Es ist unbedingt erforderlich, dass das Hineinzoomen über den Schieberegler h erfolgt! Ggf. muss man das im Unterricht das erste Mal vormachen. Wenn jemand - Google Earth geprägt - versucht, mit dem Mausrad zu zoomen, wird das nicht sonderlich erfolgreich sein. Man kann zwar im linken Fenster auch so zoomen, dass der Graph-Ausschnitt linear aussieht, aber es werden z.B. nicht die Sekanten mit beeinflusst.

© funktionenlupe.de