Funktionenlupe IIa - Sekantensteigungsfunktionen
Mit der
Funktionenlupe I kann man anschaulich bei geeigneten Funktionen an jeder Stelle die
Steigung des Funktionsgraphen ermitteln (= Funktionenmikroskop) und die Steigungen der
Sekanten, abhängig von h.
Man kann nun diese gemessenen Sekantensteigungen als y-Koordinate in Punkte übertragen, die die gleiche x-Koordinate wie A haben. Damit erhält man einen Punkt Pl mit der linksseitigen Sekantensteigung als y-Koordinate und einen Punkt Pr mit der rechtsseitigen Sekantensteigung als y-Koordinate.
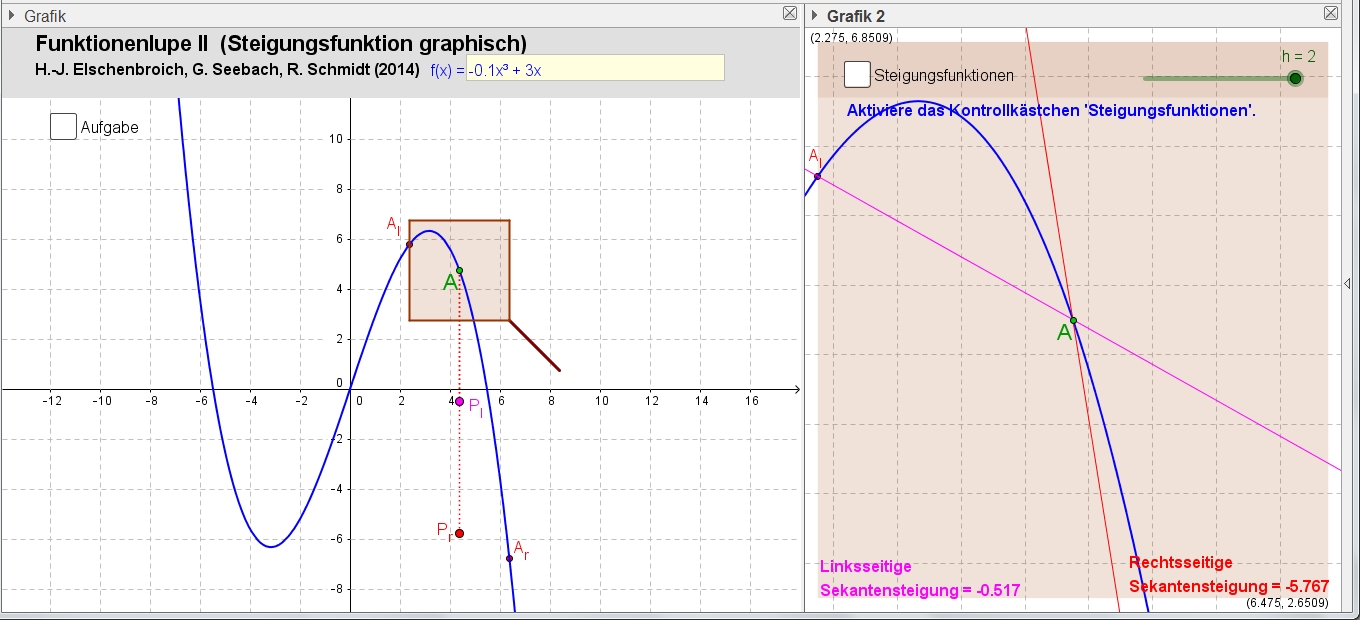
Die
Funktionenlupe II mit h = 2 |
Für größeres h sind diese Punkte in der Regel deutlich unterschiedlich, für sehr kleines h fallen sie dann (bei gutartigen Funktionen) anschaulich zusammen (Elschenbroich, 2014).
Spannend wird es, wenn man diese Punkte nun einen geometrischen Ort/ eine Ortslinie in Abhängigkeit von A zeichnen lässt. Dann erhält man die Graphen der beiden Sekantensteigungsfunktionen.
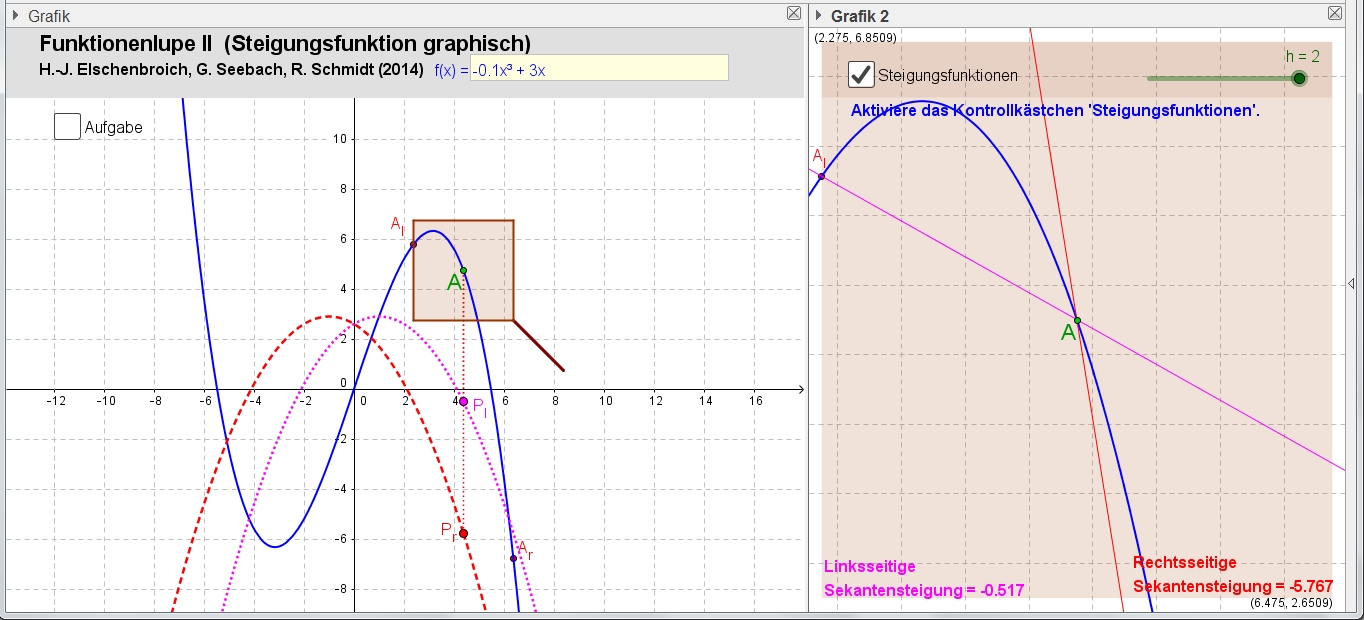
Die
Funktionenlupe II mit h = 2 |
Bei Veränderung von h werden die beiden Sekantensteigungsfunktionen simultan verändert und schachteln die Tangensteigungsfunktion ein. So bekommen wir mit der Funktionenlupe II – ohne Kenntnis des Funktionsterms von f ' – einen anschaulichen und kalkülfreien, graphischen Zugang zur Ableitungsfunktion als gemeinsamer Grenzlage der Sekantensteigungsfunktionen.
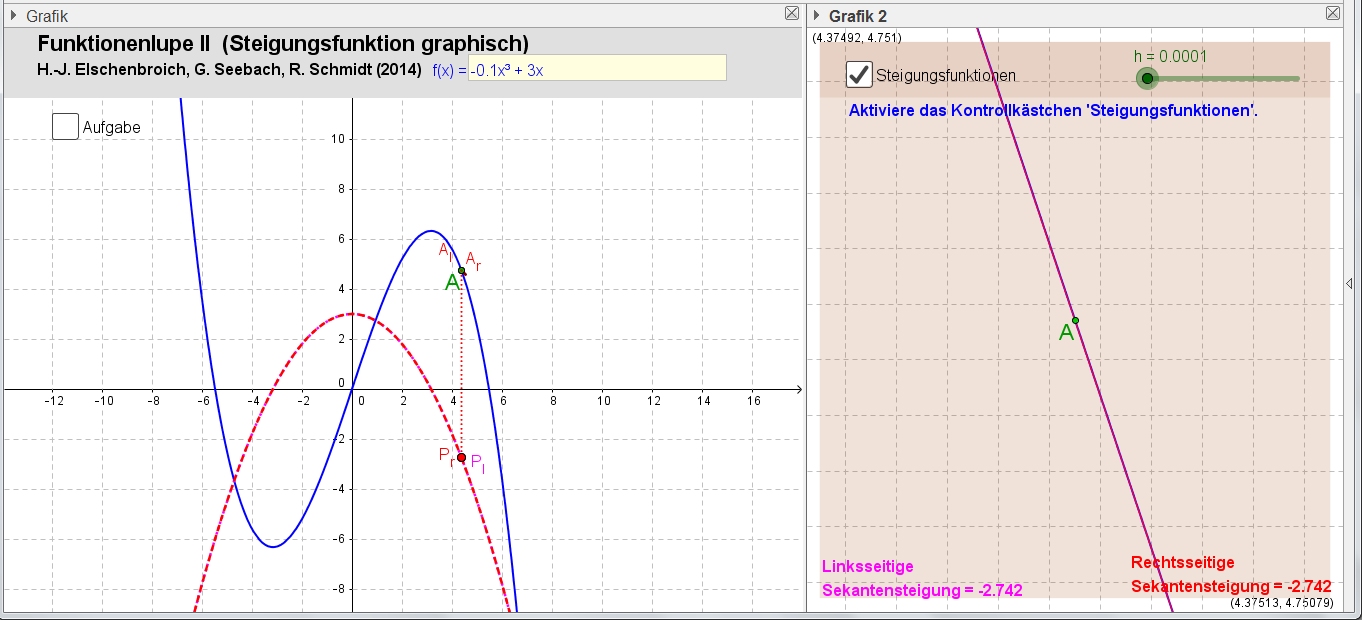
Die
Funktionenlupe II mit h = 0.0001 |
Die Steigungswerte werden im rechten Fenster angezeigt (wie bei der Funktionenlupe I), das Entscheidende passiert aber hier im linken Fenster. Durch Zugmodus und Ortslinien werden die Steigungswerte aus ihrer Lokalität herausgeholt und gewissermaßen globalisiert. Dies kann man sinnvoll nur im linken Fenster verfolgen.
Man kann nun weiter diese Ortslinien durch die Graphen der linkssseitigen und rechtsseitigen Sekantensteigungsfunktionen ersetzen, was ein Schritt zur Mathematisierung ist (und bei langsameren Rechnern auch die Performance verbessert).
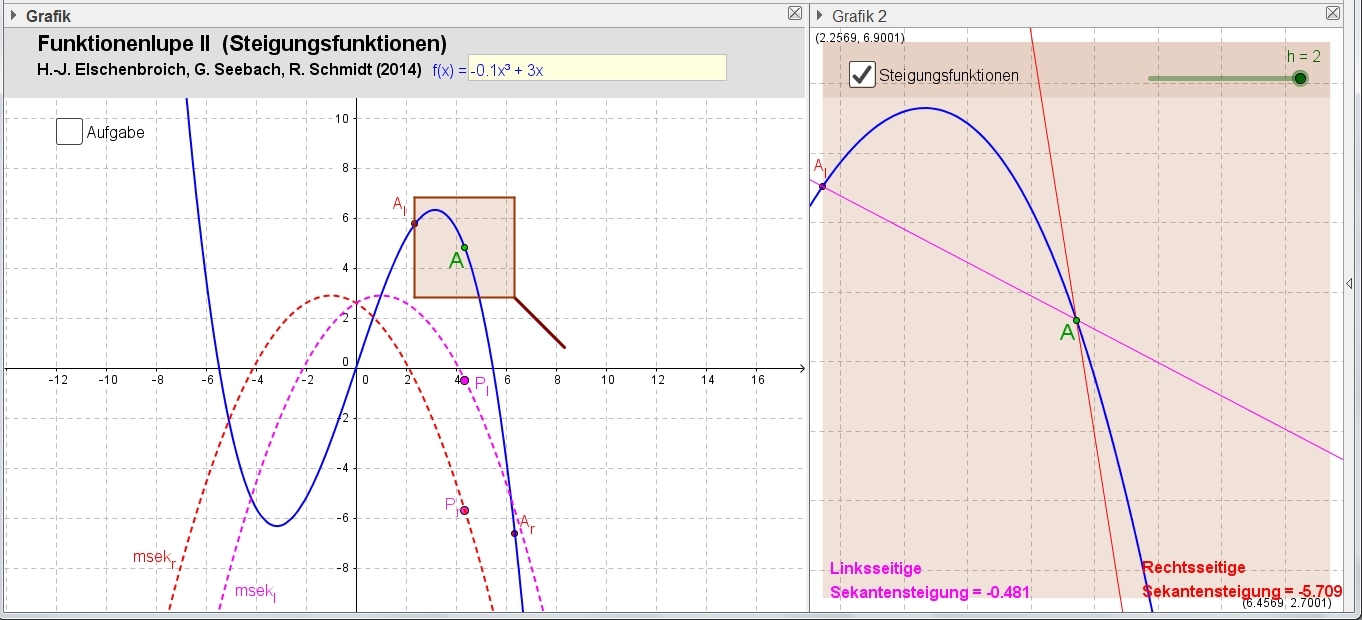
Die Funktionenlupe II mit h = 2, funktionaler Zugang msekr = (f(x+h)-f(x))/h
Dies ist ein Schritt vom graphischen Zugang zur Mathematisierung.