Funktionenlupe III - Krümmung
Analytisch ist
die Krümmung eines Graphen ein anspruchsvolles Konzept. Geometrisch ist es einfach:
Wir können
jetzt den Graphen lokal gekrümmt dadurch approximieren, dass wir (anstelle
der beiden Sekanten) durch die drei Punkte Al, A und Ar
einen Kreis konstruieren. Wird h wieder immer kleiner, so stabilisiert sich
bei gutartigen Funktionen dieser Kreis und wird anschaulich zum Schmiegekreis
(Elschenbroich 2014). Der
Kehrwert dieses Kreisradius ist betraglich die Krümmung an dieser Stelle.
Dies sieht man vor allem im linken Fenster. Im rechten Fenster sieht man zunächst die lokale Annäherung des Kreises an den Funktionsgraphen bei immer kleinerem h. Schlussendlich sieht man aber nur noch eine gemeinsame gerade Linie.
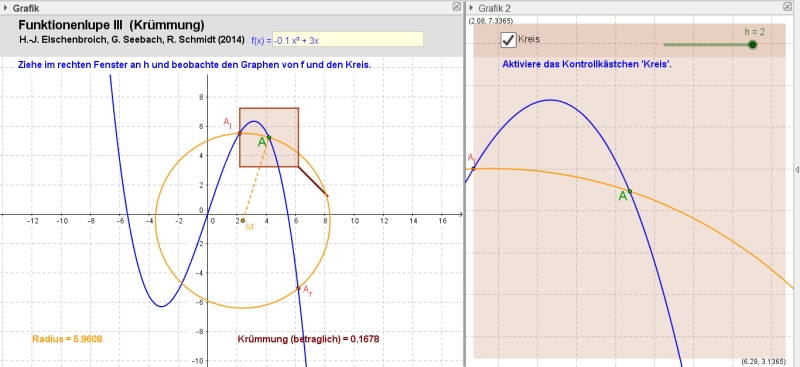
Die Funktionenlupe III mit h = 2
|
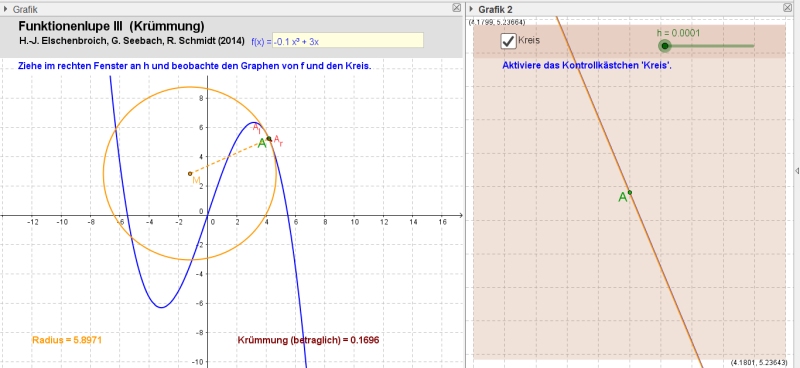
Die Funktionenlupe III mit h = 0.0001 |
So
erhalten wir einen
anschaulichen und kalkülfreien Zugang zur Krümmung. Will man noch das
Vorzeichen ermitteln, sind zusätzliche Überlegungen erforderlich
(Elschenbroich 2014), da wir über
den Kreisradius natürlich immer nur positive Werte erhalten.
Falls
die drei Punkte Al, A und Ar
auf einer Geraden liegen sollten, gibt es keinen
Kreismittelpunkt im eigentlichen Sinne. Man kann dann eine Gerade als Kreis
mit unendlichem Radius und der Krümmung Null verstehen. Dies tritt z.B. bei
der Funktion f(x) = -0.1 x³ – 3x beim Wendepunkt A = (0, 0) auf.