Funktionenlupe IV - quadratische Approximation bei f(x) = ex
Hier wird
speziell f(x) = exp(x) an der Stelle a = 0 untersucht. Man erhält für sehr
kleines h die
quadratische Funktion y = 0.5 x²+x+1.
Man bemerkt hier (natürlich nicht als Schüler, sondern mit dem Background eines Mathematik-Lehrers), dass y = x+1 für sehr kleines h anschaulich die lineare Approximation ist und sich dieser Teil nicht ändert, sondern der Summand 0.5 x² dazu kommt. So kommen wir anschaulich zum zweiten Taylorpolynom!
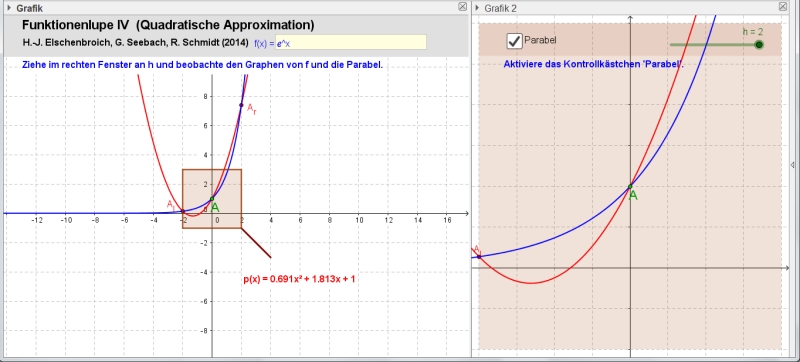
Die Funktionenlupe IV mit h = 2 für f(x) = exp(x)
|
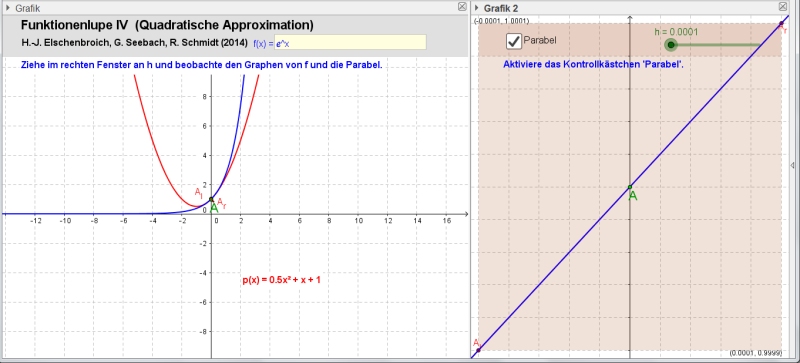
Die Funktionenlupe IV mit h = 0.0001 für f(x) = exp(x) |