Funktionenlupe VI - Bogenlänge
Analytisch ist
die Bogenlänge eines Graphen (für Schüler) durchaus ein anspruchsvolles
Konzept (das auch von den benutzten Techniken zum Bereich der Integralrechnung gehört). Geometrisch ist es
sehr einfach:
Wir können den Graphen auf einem Intervall [a; b] durch einen Sehnenzug mit n
Sehnen approximieren und dessen Länge messen. Für einen anschaulichen
Zugang reicht dies auch aus.
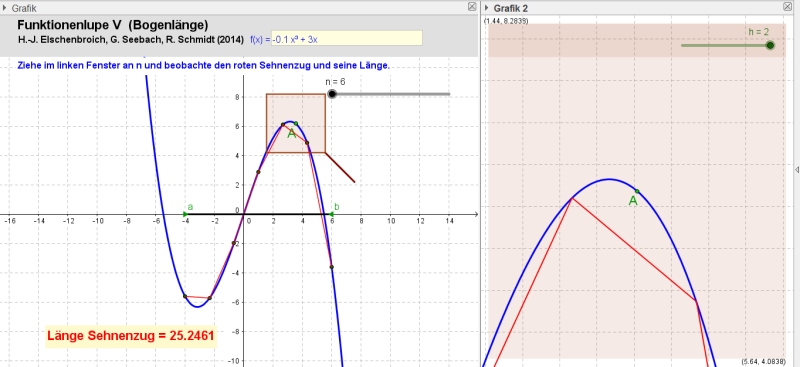
Die Funktionenlupe VI mit n = 6.
|
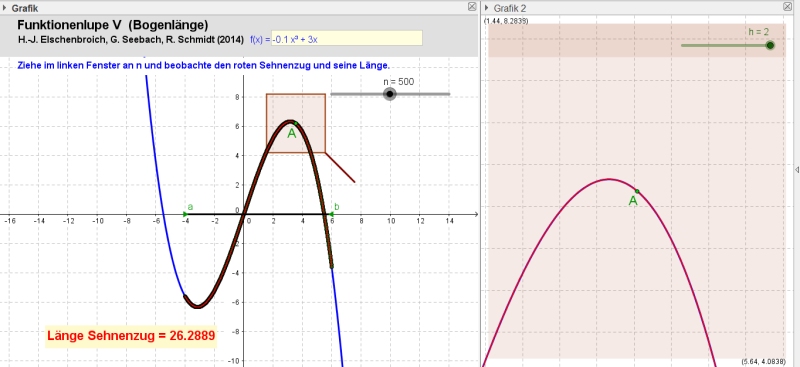
Die Funktionenlupe VI mit n = 500. |
Die Annäherung wird umso besser, je größer n
wird. Dies kann man gut im Lupenfenster sehen, wenn man mit A auf dem Graphen
von f wandert. So
erhalten wir einen
anschaulichen und kalkülfreien Zugang zur Bogenlänge (Elschenbroich 2014),
der so auch schon vor der Integralrechnung möglich ist.